MOVIMIENTO CIRCULAR : MCU Y MCUA

El Movimiento Circular Uniforme (MCU) es el movimiento que describe una partícula cuando da vueltas sobre un eje estando siempre a la misma distancia (r) del mismo y desplazándose a una velocidad constante.

Posición

La posición de la partícula depende de su posición inicial y de la velocidad a la que se desplaza. Ésta se puede calcular a partir del incremento angular, de la velocidad angular y de la velocidad tangencial (en caso de conocer las velocidades es necesario saber el tiempo t que se ha movido el cuerpo o partícula).

Velocidad angular

 

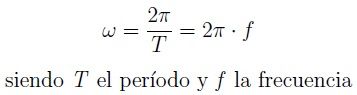En el MCU, la velocidad angular se puede calcular a partir del período o la frecuencia, ya que el período y la frecuencia son constantes.

Otra forma de determinar la velocidad angular es:

Las unidades en las que se mide la velocidad angular ω es en radianes/seg, o simplemente en s^-1.

En el MCU La velocidad angular ees constante.

Velocidad tangencial  
La velocidad tangencial es igual a la velocidad angular por el radio.


La velocidad tangencial, al igual que la velocidad angular, en el MCU es constante.

Aceleración centrípeta
A diferencia del movimiento rectilíneo uniforme, una partícula en un movimiento circular uniforme (MCU) si que tiene aceleración, la aceleración centrípeta. Esto se debe a que, aunque el módulo de la velocidad se mantiene constante, el vector cambia constantemente de dirección. 

Ésta se calcula como:

 

 

 

Aceleración angular y tangencial

En el movimiento circular uniforme (MCU), tanto la aceleración angular como la aceleración tangenciales son cero.

Período (T)

La velocidad angular en el MCU es constante, por lo que el período también será constante e irá definido por la fórmula siguiente:

Frecuencia (f)
 

La frecuencia es constante al ser constante la velocidad angular y el período:

Ejemplo

Una rueda gira a una velocidad constante de 120 revoluciones por minuto (r.p.m.). Hallar:

1. La frecuencia en ciclos/segundo.
2. La velocidad angular en radianes/segundo.
3. La velocidad tangencial en un punto de la rueda situado a 15 cm. del eje.
4. Las aceleraciones tangenciales y centrípetas en el punto citado.

Solución:

1. La frecuencia en ciclos/segundo se calcula dividiendo las r.p.m. entre los 60 segundos que tiene un minuto:
   
   
   
2. La velocidad angular (ω):
   
   
   
3. La velocidad tangencial en un punto de la rueda situado a 15 cm del eje, el radio de rotación será de r=15 cm, por lo tanto:
   
   
   
4. La aceleración tangencial es 0:
   
   
   La aceleración centrípeta en el punto citado es:
   
   
   

Movimiento circular uniformemente acelerado – MCUA

El movimiento circular uniformemente acelerado (MCUA) se presenta cuando una partícula o cuerpo sólido describe una trayectoria circular aumentando o disminuyendo la velocidad de forma constante en cada unidad de tiempo. 

Es decir, la partícula se mueve con aceleración constante.

En el dibujo se observa un ejemplo en donde la velocidad aumenta linealmente en el tiempo. Suponiendo que el tiempo en llegar del punto P₁ a P₂ sea una unidad de tiempo, la partícula viaja con una aceleración tangencial uniforme v, incrementándose esa cantidad en cada unidad de tiempo.

Velocidad angular

La velocidad angular aumenta o disminuye linealmente cuando pasa una unidad del tiempo. Por lo tanto, podemos calcular la velocidad angular en el instante t como:

El sentido de la aceleración angular α puede ser contrario al de la velocidad angular ω. Si la aceleración angular es negativa, seria un caso de movimiento circular uniformemente retardado.

Velocidad tangencial

La velocidad tangencial es el producto de la velocidad angular por el radio r. 
La velocidad tangencial también se incrementa linealmente mediante la siguiente fórmula:

Dándose aquí igualmente la posibilidad de aceleración negativa que se ha descrito en el apartado anterior.

 
Aceleración angular

La aceleración angular en el movimiento circular uniformemente acelerado es constante. Se calcula como el incremento de velocidad angular ω desde el instante inicial hasta el final partido por el tiempo.

Aceleración tangencial

La aceleración tangencial en el movimiento circular uniformemente acelerado MCUA se calcula como el incremento de velocidad v desde el instante inicial hasta el final partido por el tiempo.

 
Aceleración centrípeta
 
La aceleración centrípeta en el MCUA se halla mediante:

 

 

Componentes intrínsecas de la aceleración

La velocidad tangencial por la trayectoria en un punto P es v. En un intervalo de tiempo pequeño Δt, la velocidad incrementa a v’ en el punto P’, después de haber descrito un ángulo Δφ.
En la figura se puede ver el incremento de la velocidad tangencial Δv descompuesta en dos componentes: la tangencial Δv_t y la normal (o centrípeta) Δv_n.
Si dividimos ambas componentes de la velocidad por Δt, tendremos las componentes intrínsecas de la aceleración: la aceleración tangencial a_t y la aceleración normal a_n (o centrípeta).

Período

En el MCUA la velocidad angular cambia respecto al tiempo. 

Por tanto, el período cada vez será menor o mayor según si decrece o crece la velocidad angular.

Frecuencia

 

La frecuencia en el caso del MCUA es mayor o menor porque la velocidad angular cambia. La fórmula de la frecuencia será:

Problema

Una rueda tiene 3 m de diámetro, realiza 48 vueltas en 6 segundos. Calcula:

1. Periodo y frecuencia

2. Velocidad lineal y velocidad angular

3. Aceleración Centrípeta

Solución

a. La frecuencia:   f = número de vueltas/ tiempo empleado

                                      F = 48 v / 6 s = 8 v/s = 8 r.p.s = 8 Hz

El Periodo: T = tiempo empleado / número de vueltas

                                     T = 6 s/ 8 v = 0,75 s

 b. Velocidad Lineal o tangencial: V_t = 2 π r / T

                         V_t = 2. 3,14 . 1,5 m / 0,75 s = 9,42 m / 0,75 s = 12.56 m/s

 La velocidad Angular:  ω = 2 π / T = 2 π / 0,75 s = 2,7 π rad/s

 c. La Aceleración Centrípeta: a_c = V_t² / r = (12,56m/s)² / 1,5 m = 105,2 m/s²

Referencias web:
http://acer.forestales.upm.es/basicas/udfisica/asignaturas/fisica/animaciones.html
http://www.universoformulas.com/fisica/cinematica/movimiento-circular-uniforme/